A karácsonyi Impulzus számban átfutottunk az alapvető hallási hibákon, valamint átnéztük, miként tudjuk Fourier-spektrumban ábrázolni az elemi szinuszos függvényeket – mindez ahhoz segít hozzá minket, hogy az első digitális fényorgona projektünket befejezhessük.
Nézzük, mire kell még figyelni akkor, amikor spektrumban dolgozunk digitális környezetben, valamint azt, hogy miként következik a spektrum néhány adatából a fényerősség!
A spektrum periodicitása
Egy szemléletes, nem teljesen korrekt magyarázatot szeretnék adni arra, hogy a diszkrét jelek spektruma miért periodikus. A picit nyers, de matematikailag helyes magyarázatot Fodor György: Hálózatok és Rendszerek című könyvében találhatjátok meg.
Mi is egyáltalán a diszkrét jel? A legkézenfekvőbb definíció szerint az, amikor a jelet csak bizonyos időpontokban tudjuk leírni, nincs folyamatos információnk annak alakjáról. Mivel mi is csak mintavételezett zenét kapunk a hangkártyáról, ezért a diszkrét jelek tulajdonságai előjönnek a feldolgozás folyamán.
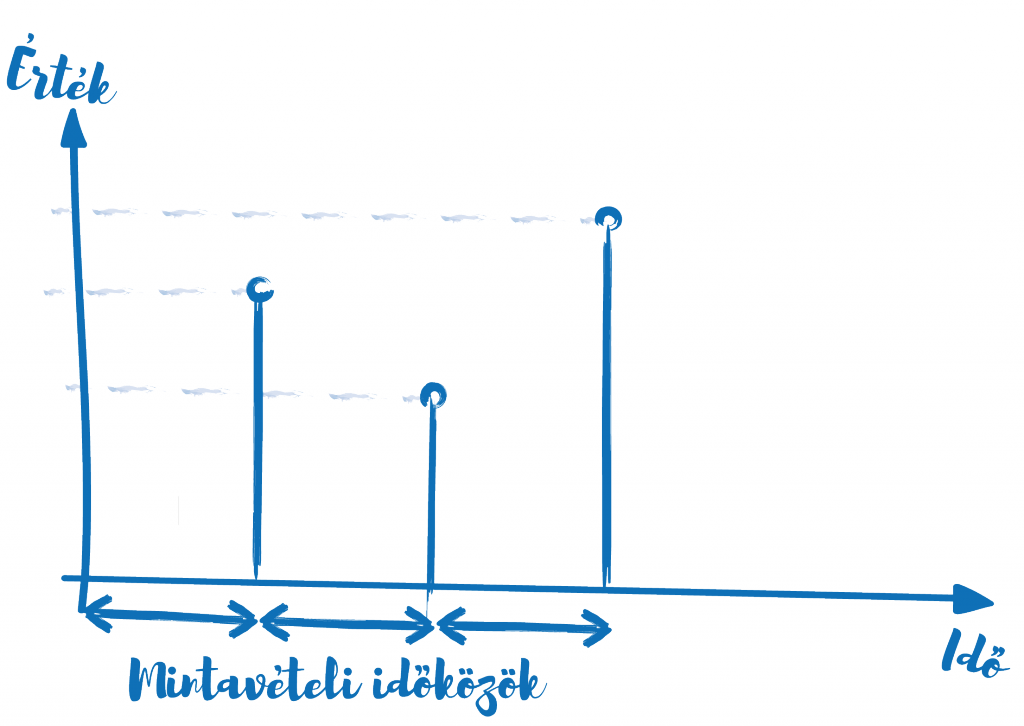
Nézzünk meg egy diszkrét jelet időtartományban! Azt látjuk magunk előtt, hogy bizonyos időpontokban erős ugrása van (a mintavételi időkben). Ha az ide vonatkozó ökölszabályokat betartva mintavételeztünk, akkor az eredeti jel minden spektrumkomponense a mintavételi frekvencia felénél is alacsonyabban van. Ez T mintavételi idő esetén azt jelenti, hogy a leggyorsabb változás is 2T időt venne igénybe. Az időtartománybeli meredek felfutás mégis jóval gyorsabb, mint 2T. Ez azt jelenti, hogy kell lennie a jelnek magasabb frekvenciakomponensű elemeinek is. A diszkretizálás folyamán azonban csak a mi jelünk megy be, illetve a mintavételi frekvencia. Mivel nem jut máshonnan információ a rendszerbe, és a kimeneti jel is következetesen azonos ugyanazon bemenetekre, ezért valahogy a bemenetekből származnak a felső frekvenciájú komponensek. Ezek alapján a kezdeti állítás annyira nem is hihetetlen, talán el tudjuk fogadni.
Miért hullámos a szinusz spektruma mégis?!
Az elmélet után vessük magunkat a gyakorlatba! Játszunk le egy szinuszt, töltsünk fel a mintákból egy tömböt, majd futtassuk a Fast Fourier Transformation függvényt! A kimeneti tömböt ábrázolva azt tapasztaljuk, hogy a szinuszunk frekvenciájánál tényleg van egy csúcs, de körülötte egy sin(x)/x-es lecsengéssel ott egy szoknya is. Miért? Vegyük észre, hogy matematikailag nem a kívánt szinuszt Fourier-transzformáltuk. Egy olyan jelet dolgoztunk fel, ami 0-tól a tömb méretéig a szinuszunk, viszont előtte és utána csupa nulla. Olyan, mintha egy négyszögimpulzussal megszoroztuk volna az egészet. Ezt figyelembe véve értékeljük az eredményt. Ami időtartományban szorzásként jelentkezik, az a transzformációs szabályok alapján frekvenciatartományban konvolúcióként. A négyszögimpulzus Fourier-transzformáltja a sin(x)/x függvény, ami ráképződik a szinuszunk kiemelkedő csúcsára.
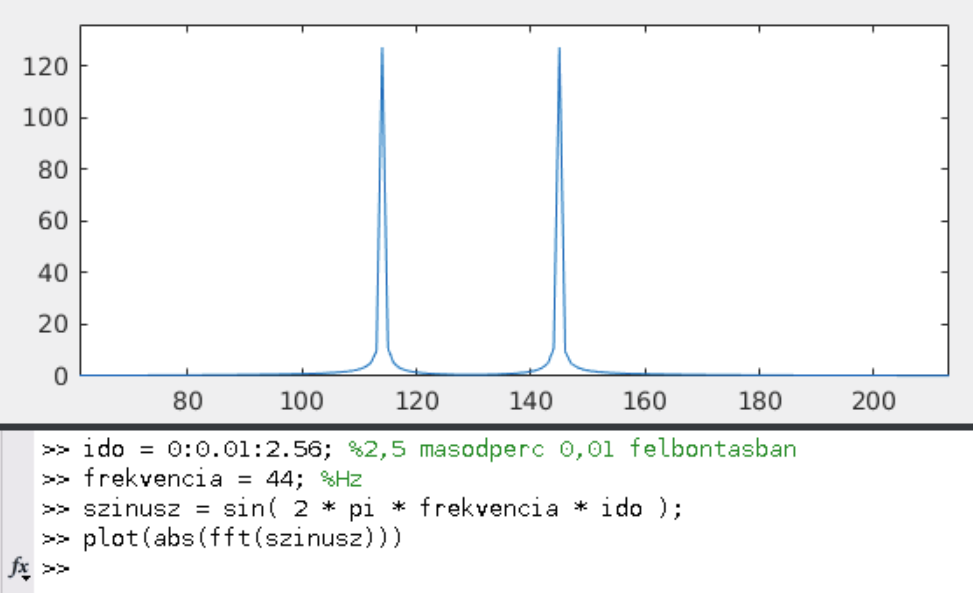
Ezt hívják az ablakozás problémájának. A szinuszunk szoknyájának a jellegén tudunk változtatni úgy, ha a tömbünket megszorozzuk egy másik ablakozófüggvénnyel transzformálás előtt, ekkor más forma konvolválódik az eredeti spektrumunkkal.
Ez a jelenség természetesen akkor is lejátszódik, ha egy sokfrekvenciás, szélessávú jelet vizsgálunk, itt viszont már nem látható annyira a változás, inkább csak az eredményt rontja minimálisan. Részletesebben az ablakozófüggvényekről az alábbi Wikipédia cikkben olvashatunk: en.wikipedia.org/wiki/Window_function
Mennyi az annyi?
A zene egy kis szeletének tudjuk a spektrális felbontását, azonban nem egy frekvencián vagyunk kíváncsiak az amplitúdóra, hanem bizonyos határok között. Valahogy össze kellene számolni, hogy „mennyi hang van” adott frekvenciák között. Érezhető, hogy nem lehet egyszerűen csak összeadni a számokat a-tól b-ig, hiszen itt szinuszokról (pontosabban komplex kitevős hatványokról) beszélünk. Szerencsére ennek a problémának is van egy szemléletes megoldása. A kulcs az ortogonalitás: egy ismert frekvenciájú szinuszt akármilyen módon szorzunk, osztunk, tolunk, nem tudunk másik frekvenciájút előállítani belőle. Fogjuk fel úgy a feldolgozott jelszeletet, mint egy vektor N darab egymástól független koordinátáját! Azt, hogy az adott jelszelet mennyire erős (mekkora a vektor) Pitagorasz-tétel szerint tudjuk számolni. A probléma megoldása tehát az, hogy a jelek négyzetösszegét kell képezni a kívánt sávban. Matematikai precizitással Perseval fogalmazta meg és bizonyította a fenti állítást.
Kísérletezés útján a következő frekvenciasávokhoz juthatunk:
- 50-160 Hz-ig mélynek érezzük a hangokat
- 140-2500 Hz-ig középmagasnak érezzük a hangokat
- 2000-6000 Hz-ig magasnak érezzük a hangokat.
Mi történik akkor, ha egy erős kitartott hang épp egy sáv széle körül remeg? Erősen villogni fog az a szín. Épp ezért a sávok szélén lévő hangok erősségét kisebb súllyal szokták figyelembe venni, azaz a Pitagorasz-tételes összegzés előtt egy ablakozófüggvénnyel megszorozzák azt a sávot.
A hallás sajátosságainak figyelembe vétele
Normálás
Annak érdekében, hogy könnyű legyen bánni a számokkal, skálázzuk át őket 0 és 1 közé. Ehhez tudnunk kell sávonként a teljesítményértékek minimum-, illetve maximumértékékét. Ha folyamatában dolgozzuk fel az adatokat, akkor egy viszonylag rövid idő után előkerülnek minimum-, illetve maximum közeli értékek. Ezeket a programunkban két egyszerű változóban el lehet tárolni. Az eddig előfordult legkisebb teljesítmény jelentse a 0-t, a legnagyobb az 1-et.
Ezzel egyébként rögtön kiküszöböltük azt, hogy a különböző hangerejű zenék eltérő intenzitással képződjenek le színekre. Mellékesen a normálás a különböző színekre külön-külön dolgozik, de ez nem feltétlenül probléma.
Utóelnyomás és halk részek
A fent használt normálás kis módosítással ezeket a problémákat is megoldja. Mindössze azt kell figyelni, hogy ha a legutóbbi időben csak mondjuk 0.8 fölötti érték volt, akkor a normálás alsó határát kezdjük el növelni. Ezzel lekezeljük azt, hogy a fülünk „kezd hozzászokni a hangerőhöz”. A halk részeknél is rááll a fülünk a zenére. Itt arra kell figyelnünk, hogy ha a zene sokáig például 0.2 alatt van, akkor kezdjük el csökkenteni a normálás tetejét.
Videószűrés
A zenékben nagyon gyakoriak az éles váltások, főleg a modern darabokban. Nem lenne kellemes, ha az egészséges ember is epilepsziás rohamot kapna a szórakoztatóelektronikai eszközöktől, ezért ez ellen tenni kell valamit. A villanykörtés időszakban ez magától megoldódott. A villanykörte izzószála nem tudott azonnal kihűlni, tartotta a meleget. Kellően lassan aludt ki ahhoz, hogy ne legyen zavaró, de kellően gyorsan ahhoz, hogy még tudja követni a zenét.
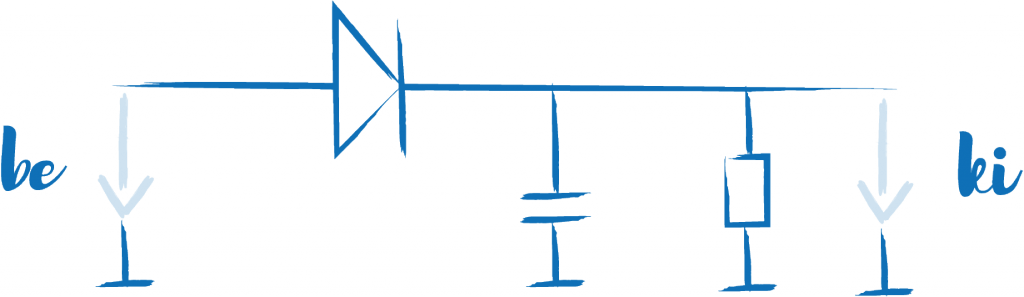
A csúcsegyenirányító kapcsolási rajza
A modern LED-ek viszont gyorsan kialszanak, nekünk kell megoldani a problémát. Analóg elektronikában jártas emberekben felmerülhet egy csúcsegyenirányító használata. Ezzel megoldanánk a problémát, viszont most egy virtuális világban vagyunk, ahol csak azokat a műveleteket tudjuk végezni, amiket a processzor támogat. Szerencsére a csúcsegyenirányító működését nem nehéz szimulálni. Ha a bemenet nagyobb, mint a tároló (általában kondenzátor) által nyújtott érték, akkor a bemenet értékét vegye fel a tároló. Amennyiben épp alacsonyabb a bejövő jel, akkor egy terhelés csökkentse a tároló értékét (általában ellenállás). A csökkentést úgy tudjuk megoldani digitálisan, ha egy egynél kisebb számmal megszorozzuk a tároló értékét. Ekkor egy exponenciális lecsengést kapunk a kimeneten, ami 0-hoz tart (ez ugye egy mértani sorozat határértéke).
Megjelenítés
Az így kapott számokat vagy a számítógép képernyőjén vagy egy speciálisabb kijelzőn ábrázoljuk.
Végeredmény
Az alábbi videókon két fényorgonát is láthatunk. Az egyik egy tisztán analóg áramköri megvalósítás, a másik pedig a Schönherz mátrix egy darabját használja megjelenítésre. Utóbbit a Szakkoholischták csapat vette fel a QPA indulójukhoz.